Kiểm tra - cuối khóa
Bài mở đầu
Nộp bàiBạn hãy in ra cụm từ TDZ ra màn hình \(20\) lần, các cụm từ cách nhau một dấu cách.
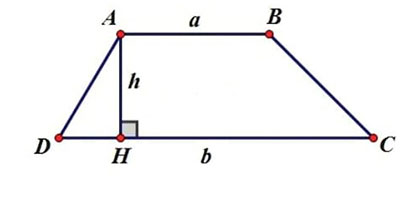
Hình thang
Nộp bàiCho \(a, b\) là độ dài 2 cạnh đáy và \(h\) là chiều cao của một hình thang. Tính diện tích hình thang đó.
Input
- Gồm một dòng chứa \(3\) số thực \(a, b, h\) (\(a, b, h \leq 1000\)).
Output
- In ra diện tích hình thang. Kết quả được tính đến chữ số thập phân thứ 3.
Sample Test
Input
5 3 2
Output
8
Phân số
Nộp bàiCho bốn số nguyên dương \(a, b, c, d\). Hãy so sánh \(\frac {a} {b}\) với \(\frac {c} {d}\).
Input
- Gồm một dòng chứa bốn số nguyên dương \(a, b, c, d\) (\(a, b, c, d \leq 10^9\)).
Output
- In ra
>nếu \(\frac {a} {b} > \frac {c} {d}\). - In ra
<nếu \(\frac {a} {b} < \frac {c} {d}\). - In ra
=nếu \(\frac {a} {b} = \frac {c} {d}\).
Sample Test
Input
1 2 3 4
Output
<
Note
- \(\frac {1} {2} < \frac {3} {4}\).
Số may mắn
Nộp bàiTDZ quan niệm rằng, một số không may mắn là số chia hết cho \(5\) hoặc chia cho \(5\) dư \(3\).
Vi dụ các số may mắn: \(1, 2, 4, 6, 7, 9, 11, 12, 14\).
Biết rằng TDZ chỉ sử dụng tất cả các số may mắn nhỏ hơn \(N\) đánh số thứ tự các bạn học sinh để gửi lời chúc kiểm tra thật tốt. Hãy tính tổng các số may mắn đã được sử dụng.
Input
- Gồm một số nguyên dương \(N\) duy nhất. (\(N \leq 10^8\))
Output
- In ra tổng các số may mắn nhỏ hơn \(N\).
Sample Test
Input
15
Output
66
Note
- Các số may mắn nhỏ hơn \(N\) là \(1, 2, 4, 6, 7, 9, 11, 12, 14\) và tổng của chúng bằng \(66\).
Đèn LED
Nộp bàiTrên một màn hình LED lớn, người ta lần lượt cho hiện ra các số tự nhiên từ \(0\) đến \(9\) và cứ lặp đi lặp lại như thế (tức là sau số \(9\) là số \(0\)).
Ban đầu, giây thứ \(0\), màn hình xuất hiện số \(K\) \((0 ≤ K ≤ 9)\), sau \(1\) giây sẽ chuyển số tiếp theo.
Hỏi sau \(N\) giây, màn hình đang hiển thị số mấy?
Yêu cầu: Nhập vào \(N, K\). In ra số đang hiển thị ở giây thứ \(N\).
Input
- Gồm hai số nguyên \(N, K\) \((K \le 9; N \le 10^9)\).
Output
- In ra một số nguyên duy nhất là kết quả của bài toán.
Sample Test
Input
5
0
Output
5
Tổng lẻ bình phương
Nộp bàiCho một số nguyên dương \(n\). Hãy tính và in ra tổng bình phương của các số lẻ từ \(1\) đến \(n\).
Input
- Dòng đầu tiên chứa số nguyên dương \(n\) \((1 \leq n \leq 10^3)\).
Output
- In ra kết quả của bài toán
Sample Test
Test 1
Input
5Output
35Test 2
Input
10Output
165Đầu và cuối
Nộp bàiCho một từ chỉ gồm các chữ cái tiếng Anh. Hãy in ra chữ cái đầu tiên và cuối cùng của từ đó.
Input
- Gồm một dòng chứa một từ có độ dài không quá 200.
Output
- In ra chữ cái đầu tiên và cuối cùng của từ đó.
Sample Test
Test
Input
ThreeOutput
T eChữ số nguyên tố
Nộp bàiCho số nguyên dương \(N\). Đếm xem trong các chữ số của \(N\) có bao nhiêu số nguyên tố.
Input
- Gồm một số nguyên dương \(N\) duy nhất.
Output
- In ra số lượng chữ số là số nguyên tố trong \(N\).
Subtasks
- Subtask 1 (\(50\%\) số điểm): \(N \leq 10^4\).
- Subtask 2 (\(20\%\) số điểm): \(N \leq 10^8\).
- Subtask 3 (\(30\%\) số điểm): \(N \leq 10^{100}\).
Sample Test
Input
23452345
Output
6
Note
- Có \(6\) chữ số nguyên tố trong \(N\) là \(2, 3, 5, 2, 3, 5\).
Số đơn lẻ
Nộp bàiCho một dãy gồm \(N\) số nguyên dương \(a_1, a_2, a_3, ..., a_N\). Biết rằng các số trong dãy đều xuất hiện hai lần, trừ một số. Hãy tìm số đó.
Input
- Dòng thứ nhất chứa số nguyên dương \(N\).
- Dòng thứ hai chứa \(N\) số nguyên dương \(a_1, a_2, a_3, ... a_N\). (\(a_i \leq 10^6\))
- Các số đều xuất hiện hai lần trừ một số.
Output
- In ra số chỉ xuất hiện một lần trong dãy.
Subtasks
- Subtask 1 (\(20\%\) số điểm): \(N = 3\).
- Subtask 2 (\(30\%\) số điểm): \(N \leq 10^3\).
- Subtask 3 (\(50\%\) số điểm): \(N \leq 10^6\).
Sample Test 1
Input
5
4 1 2 1 2
Output
4
Hoán vị số
Nộp bàiNguồn: Học sinh Giỏi THPT Hà Nội năm 2020 - 2021
Trong một cuốn sách cổ có ghi lại rất nhiều các con số bí ẩn mà chúng có mối liên hệ với số \(30\). Sau một thời gian nghiên cứu, các chuyên gia đã tìm được cách giải mã các số đó: hoán vị các chữ số của số bí ẩn để thu được một bội số lớn nhất của \(30\).
Yêu cầu: Hãy viết chương trình để giúp các chuyên gia giải mã các số bí ẩn đó.
Input
Dữ liệu vào từ tệp văn bản BAI2.INP:
- Gồm một dòng duy nhất chứa số nguyên dương \(N\), với \(N\) có tối đa \(10^7\) chữ số là số cần giải mã.
Output
Kết quả ra tệp văn bản BAI2.OUT:
- Gồm một số nguyên duy nhất là số lớn nhất chia hết cho \(30\) tìm được bằng cách hoán vị các chữ số của \(N\). Nếu không tìm thấy thì đưa ra
-1.
Example
Test 1
Input
1002Output
2100Note
- Số \(2100\) là hoán vị lớn nhất của số \(1002\) và chia hết cho \(30\).
Test 2
Input
12498567859Output
-1Note
- Không tồn tại số hoán vị nào chia hết cho \(30\).
Constraint
- Có \(50\%\) số test: \(N \leq 10^7\);
- Có \(50\%\) số test còn lại: \(N\) có tối đa \(10^9\) chữ số.
Dãy số có quy luật
Nộp bàiCho dãy số có quy luật như sau: \(1,2,2,3,3,3,4,4,4,4,5,5,…\)
Cho một số tự nhiên \(N\), hãy tìm số thứ \(N\) của dãy số trên (các số được đánh thứ tự từ \(1\)).
Input
- Gồm một số nguyên dương \(N\) \((N ≤ 10^{15})\).
Output
- In ra kết quả của bài toán.
Subtasks
- Subtask 1 (\(60\%\) số điểm): \(N ≤ 10^{6}\);
- Subtask 2 (\(20\%\) số điểm): \(N ≤ 10^{10}\);
- Subtask 3 (\(20\%\) số điểm): Không có ràng buộc gì thêm.
Sample Test
Input
5
Output
3
Xâu con chia hết cho 4
Nộp bàiCho một xâu \(S\) gồm các kí tự số. Hãy đếm xem có bao nhiêu xâu con chia hết cho \(4\) (xâu con có thể bắt đầu bằng \(0\)).
Một xâu con của \(S\) là xâu được tạo thành từ các ký tự liên tiếp trong \(S\).
Input
- Gồm một xâu \(S\) có độ dài không quá \(10^6\).
Output
- In ra kết quả của bài toán.
Subtasks
- Subtask 1 (\(60\%\) số điểm): Xâu \(S\) có độ dài không quá \(100\).
- Subtask 2 (\(40\%\) số điểm): Không có ràng buộc gì thêm.
Sample Test 1
Input
08
Output
3
Note
- Các xâu con thoã mãn là \(0, 8, 08\).
Sample Test 2
Input
13085
Output
5
Tổng các ước
Nộp bàiSố nguyên dương \(d\) được gọi là ước của số nguyên dương \(N\) nếu \(N\) chia hết cho \(d\). Ví dụ: các ước của \(9\) là \(1, 3\) và \(9;\) các ước của \(10\) là \(1, 2, 5\) và \(10\).
Yêu cầu: Cho hai số nguyên dương \(L\) và \(R\) \((L ≤ R)\). Hãy tính tổng của tất cả các số nguyên dương là ước của ít nhất một số trong đoạn từ \(L\) tới \(R\) \((\)bao gồm cả \(L\) và \(R)\).
Dữ liệu vào từ tệp văn bản SUMDIV.INP:
Gồm một dòng chứa hai số nguyên dương \(L\) và \(R\) \((1 ≤ L ≤ R ≤ 10^9).\)
Kết quả ghi ra tệp văn bản SUMDIV.OUT:
Một số nguyên duy nhất là tổng của tất cả các số nguyên dương là ước của ít nhất một số trong đoạn từ \(L\) tới \(R\).
Ràng buộc
- Có \(20\%\) số test ứng với \(R ≤ 1000\);
- \(25\%\) số test khác ứng với \(R - L ≤ 1000\);
- \(25\%\) số test khác ứng với \(R ≤ 10^6\);
- \(30\%\) số test còn lại không có điều kiện gì thêm.
Ví dụ
Input
9 12
Output
63
Giải thích
Các số là ước của ít nhất một số trong đoạn \([9, 12]\) là: \(1, 2, 3, 4, 5, 6, 9, 10, 11\) và \(12\) \((7\) và \(8\) không nằm trong danh sách này vì cả \(9, 10, 11\) và \(12\) đều không chia hết cho \(7\) hoặc \(8)\).
Ta có \(1 + 2 + 3 + 4 + 5 + 6 + 9 + 10 + 11 + 12 = 63\).
Input
7 7
Output
8
Giải thích
Các số là ước của \(7\) là \(1\) và \(7\). Ta có \(1 + 7 = 8\).
Chọn dãy
Nộp bàiCho dãy số \(A\) gồm \(N\) phần tử, và một số \(K\). Ta có thể chọn một dãy con sao cho vị trí các phần tử được chọn cách nhau tối thiểu \(K\) đơn vị.
Tìm tổng lớn nhất có thể đạt được.
Input
- Dòng 1 gồm 2 số \(N\) và \(K\) \((N, K \le 10^5)\)
- Dòng 2 gồm \(N\) số là giá trị các số trong dãy \(A\) \((A[i] \le 10^5)\).
Output
- Một số duy nhất là kết quả của bài toán
Subtask
- Subtask \(1\) (\(25\%\) số điểm): \(n, k \le 20\)
- Subtask \(2\) (\(5\%\) số điểm): \(n = k\)
- Subtask \(3\) (\(15\%\) số điểm): Các phần tử có giá trị bằng nhau
- Subtask \(4\) (\(30\%\) số điểm): \(n, k \le 10^3\)
- Subtask \(5\) (\(25\%\) số điểm): \(n, k \le 10^5\)
Sample
Test 1
Input
5 3
2 4 3 5 1Output
7Note
- Ta có thể chọn dãy gồm 2 phần tử: \(A_1 = 2\) và \(A_4 = 5\). Hai phần tử này nằm ở vị trí cách nhau đùng \(3\) đơn vị, và có tổng là \(7\).