PreHNOI 2
Đếm đường
Nộp bàiCho một bảng có kích thước \(N \times M\), các hàng được đánh số từ \(1\) đến \(N\) từ trên xuống dưới, các cột được đánh số từ \(1\) đến \(M\) từ trái sang phải, ô ở hàng \(i\) cột \(j\) kí hiệu là ô \((i, j)\). Ở mỗi vị trí \((i, j)\) có giá trị \(A_{i, j}\). Một đường đi từ \((1, 1)\) đến \((N, M)\) được gọi là hợp lệ nếu:
- Chỉ đi sang phải hoặc xuống dưới.
- Giá trị ở ô tiếp sau đó phải có giá trị lớn hơn ô hiện tại.
Gọi \(f(A)\) là số đường đi hợp lệ khác nhau với bảng giá trị \(A\). Hai đường đi được gọi là khác nhau nếu tồn tại ít nhất một ô xuất hiện trong đường đi này mà không xuất hiện trong đường đi kia.
Hãy tính tổng \(f(A)\) với mọi bảng giá trị \(A\) khác nhau thỏa mãn \(1 \le A_{i,j} \le K\), modulo \(998244353\).
Input
- Một dòng duy nhất chứa ba số nguyên dương \(N\), \(M\) và \(K\), cách nhau một dấu cách.
Output
- Một số nguyên duy nhất là đáp án modulo \(998244353\).
Scoring
Trong mọi test, \(1 \le N \le 2 \times 10^5\), \(1 \le M \le 2 \times 10^5\), \(1 \le K \le 10^9\)
- Subtask 1 \((20\%)\): \(N \times M \le 20\) và \(K \le 2\);
- Subtask 2 \((20\%)\): \(N, M \le 3000\) và \(K = 1\);
- Subtask 3 \((15\%)\): \(K = 1\);
- Subtask 4 \((20\%)\): \(N = 1\) và \(M, K \le 3000\);
- Subtask 5 \((15\%)\): \(N = 1\);
- Subtask 6 \((10\%)\): Không có giới hạn gì thêm.
Example
Test 1
Input
1 3 2Output
4Test 2
Input
3 4 3Output
204120Cây Khô Gà
Nộp bàiGiới thiệu về anh Độ
Chào mừng bạn đã trúng tuyển vào vị trí Trưởng Kho Kế Toán tại Tổng Công Ty MixiFood. Công ty có \(n\) thành viên, tạo thành một cây cấu trúc phân cấp, với CEO Tộc Trưởng Độ (thành viên số 1) là người đứng đầu.
Nhiệm vụ của bạn là theo dõi số lượng khô gà trong kho của mỗi thành viên. Khi mới bắt đầu, kho của tất cả mọi người đều trống không (giá trị bằng 0). Bạn sẽ phải xử lý \(q\) hoạt động phân phối và kiểm kê của công ty.
Truy vấn
Có 2 loại hoạt động chính bạn cần ghi chép:
-
Truy vấn loại 1:
1 v x k- Trưởng phòng \(v\) nhận và phân phối lô hàng mới.- Một lô hàng khô gà mới về. Trưởng phòng \(v\) là người chịu trách nhiệm chính và nhận trực tiếp một lượng là \(x\), gọi là "Lô Hàng Gốc".
- Sau đó, \(v\) sẽ phân phối xuống cho các nhân viên cấp dưới (hậu duệ) của mình. Một nhân viên ở cách \(v\) một khoảng cách \(i\) (số cạnh trên đường đi ngắn nhất) sẽ nhận được \(x - i \cdot k\) gói (lượng này có thể nhỏ hơn \(0\)).
- Ở đây, \(k\) là một chỉ số cực kỳ quan trọng, được gọi là "Chỉ Số Rơi Vãi". Nó đại diện cho số gói bị thất lạc hoặc... bị các sếp ăn bớt trên mỗi cấp trung gian.
-
Truy vấn loại 2:
2 v- Kiểm toán đột xuất.- Tộc trưởng muốn biết chính xác tại thời điểm này, thành viên \(v\) đang tồn kho bao nhiêu gói khô gà.
- Vì số lượng khô gà có thể cực kỳ lớn, Tộc trưởng chỉ yêu cầu bạn báo cáo con số sau khi đã lấy phần dư cho \(10^9 + 7\).
Input từ file mixi.inp
- Dòng đầu tiên chứa số nguyên \(n\) (\(1 \le n \le 5 \cdot 10^5\)) — tổng số thành viên của MixiFood.
- Dòng thứ hai chứa \(n - 1\) số nguyên \(p_2, p_3, \dots, p_n\) (\(1 \le p_i < i\)), với \(p_i\) là sếp trực tiếp của thành viên \(i\).
- Dòng thứ ba chứa số nguyên \(q\) (\(1 \le q \le 5 \cdot 10^5\)) — số lượng hoạt động cần xử lý.
- \(q\) dòng tiếp theo, mỗi dòng mô tả một hoạt động:
- Nếu là hoạt động phân phối:
1 v x k(\(1 \le v \le n, 0 \le x, k < 10^9 + 7\)). - Nếu là hoạt động kiểm toán:
2 v(\(1 \le v \le n\)).
- Nếu là hoạt động phân phối:
Output ra file mixi.out
Với mỗi hoạt động kiểm toán (loại 2), hãy in ra tổng lượng khô gà hiện có của thành viên tương ứng trên một dòng duy nhất, sau khi đã lấy modulo \(10^9 + 7\).
Scoring
- Subtask 1 (20% điểm): \(n, q \le 2000\)
- Subtask 2 (20% điểm): \(n, q \le 50000\).
- Subtask 3 (20% điểm): Chỉ Số Rơi Vãi \(k = 0\) trong mọi đợt phân phối
- Subtask 4 (20% điểm): \(n, q \le 2 \cdot 10^5\).
- Subtask 5 (20% điểm): MixiFood trở thành tập đoàn toàn cầu, không giới hạn gì thêm.
Ví dụ
Test 1
Input
3
1 1
3
1 1 2 1
2 1
2 2Output
2
1Giải thích ví dụ:
- Cây có 3 đỉnh. Đỉnh 2 và 3 là con của đỉnh 1. Ban đầu:
[0, 0, 0]. - Truy vấn
1 1 2 1: - Đỉnh 1 (khoảng cách 0) cộng thêm
2 - 0*1 = 2. Mảng:[2, 0, 0]. - Đỉnh 2 là hậu duệ của 1 ở khoảng cách 1, cộng thêm
2 - 1*1 = 1. Mảng:[2, 1, 0]. - Đỉnh 3 là hậu duệ của 1 ở khoảng cách 1, cộng thêm
2 - 1*1 = 1. Mảng:[2, 1, 1]. - Truy vấn
2 1: In ra giá trị của đỉnh 1 là2. - Truy vấn
2 2: In ra giá trị của đỉnh 2 là1.
Sparky
Nộp bàiVới sự góp sức của người dân, vùng đất CB đã xây thêm rất nhiều cầu bắc qua sông mới. Trong hành trình của mình, Sparky cần băng qua một dòng sông có \(K\) làn cầu. Vì con sông rất dài, mỗi làn cầu lại có \(N + 1\) trạm thu phí (\(1\) trạm ở đầu, cuối và \(N - 1\) trạm ở giữa) được đánh số từ \(1\) đến \(N + 1\). Sparky được thông báo thời gian đi qua hai trạm \((i, j)\) và \((i + 1, j)\) ở làn \(j\) là \(A_{i, j}\). Đồng thời, Sparky cũng có thể chuyển giữa hai làn cầu cạnh nhau với chi phí thời gian là \(X\). Sparky cần đi qua sông với thời gian ngắn nhất, nên cậu không quan tâm mình đang ở làn cầu nào, miễn là cậu có thể đi qua \(N + 1\) trạm thu phí. Nói cách khác, Sparky muốn biết thời gian ít nhất để đi từ trạm thu phí \(1\) ở bất cứ làn nào đến trạm \(N + 1\) ở bất cứ làn nào.
Tuy nhiên, do vướng phải lịch thi công của các điểm trường mới, \(Q\) giả định được đưa ra. Với mỗi giả định \(j\) ở làn cầu \(Y_j\), một trạm \(X_j\) sẽ đóng cửa để đảm bảo thi công điểm trường, tức Sparky sẽ không thể đi từ trạm \(X_j\) đến \(X_j + 1\) trên làn cầu \(Y_j\). Với \(Q = 0\), sẽ không có giả định nào được đưa ra.
Input từ file sparky.inp
Dòng đầu tiên chứa ba số nguyên dương \(N, K, X\) (\(1 \le N, K \le 2 \times 10^6, N \times K \leq 10^6, X \leq 10^9\)) là số trạm, số làn cầu và chi phí chuyển làn tương ứng.
\(N\) dòng tiếp theo, mỗi dòng chứa \(K\) số nguyên \(A_{i, j} (1 \leq i \leq N, 1 \leq j \leq K)\) là chi phí để di chuyển giữa 2 trạm thu phí \((i, j)\) và \((i + 1, j)\) ở làn \(j\).
Dòng tiếp theo chứa số nguyên dương \(Q\) \((0 \le Q \le 10^6)\).
\(Q\) dòng tiếp theo, dòng thứ \(j\) chứa hai số nguyên dương \(X_j, Y_j\) là trạm thu phí đóng cửa ở giả định thứ \(j\).
Output ra file sparky.out
In ra \(Q + 1\) dòng, dòng thứ \(i \ (0 \leq i \leq Q)\) gồm một số nguyên là đáp án ở giả định tứ \(i\).
Scoring
- Subtask 1 \((12\%)\): \(N \leq 10, K \leq 2, Q = 0\);
- Subtask 2 \((12\%)\): \(N \leq 10, K \leq 10, Q = 0\);
- Subtask 3 \((12\%)\): \(N \leq 100, K \leq 300, Q = 0\);
- Subtask 4 \((12\%)\): \(N \leq 100, K \leq 300, Q \leq 100\);
- Subtask 5 \((12\%)\): \(N \leq 100, K \leq 10^4, Q = 0\);
- Subtask 6 \((12\%)\): \(N \leq 100, K \leq 10^4, Q \leq 10^4\);
- Subtask 7 \((28\%)\): Không có ràng buộc gì thêm;
Ví dụ
Test 1
Input
5 4 2
2 3 4 2
1 1 2 3
1 2 1 3
1 3 4 4
1 3 2 4
3
4 1
3 1
1 2Output
6
12
10
6Kindred
Nộp bàiSau khi full đề IOI 2026, Hải bắt đầu tập chơi tựa game Liên Minh Huyền Thoại. Trong game có hai đội, mỗi đội 5 người, và mỗi người chơi điều khiển một tướng khác nhau.
Chơi game được một thời gian, Hải trở nên yêu thích Kindred - một con tướng có bộ chiêu thức khá hay. Sau khi chơi đủ 1000 ván Kindred, Hải liền nghĩ ra bài toán sau:
Mỗi tướng được đặc trưng bởi hai số nguyên \(h\) và \(H\) - HP (health power) hiện tại và HP tối đa của tướng đó.
- Khi HP của tướng rơi xuống dưới hoặc bằng \(0\) (\(h \le 0\)), tướng đó sẽ chết và phải đợi hồi sinh.
- Khi HP của tướng sau khi hồi lại \(x\) HP mà lớn hơn mức HP tối đa \((h + x > H)\), thì HP của tướng sẽ được đặt lại thành \(H\).
Trong giao tranh, HP của tướng có thể bị giảm hoặc hồi lại. Cho \(n\) hành động trong giao tranh, hành động thứ \(i\) sẽ tác động đến HP của tướng một lượng là \(a_i\).
- Nếu \(a_i > 0\) thì tướng được hồi một lượng HP là \(a_i\).
- Nếu \(a_i = 0\) thì HP không đổi.
- Nếu \(a_i < 0\) thì tướng bị tấn công và mất \(a_i\) HP.
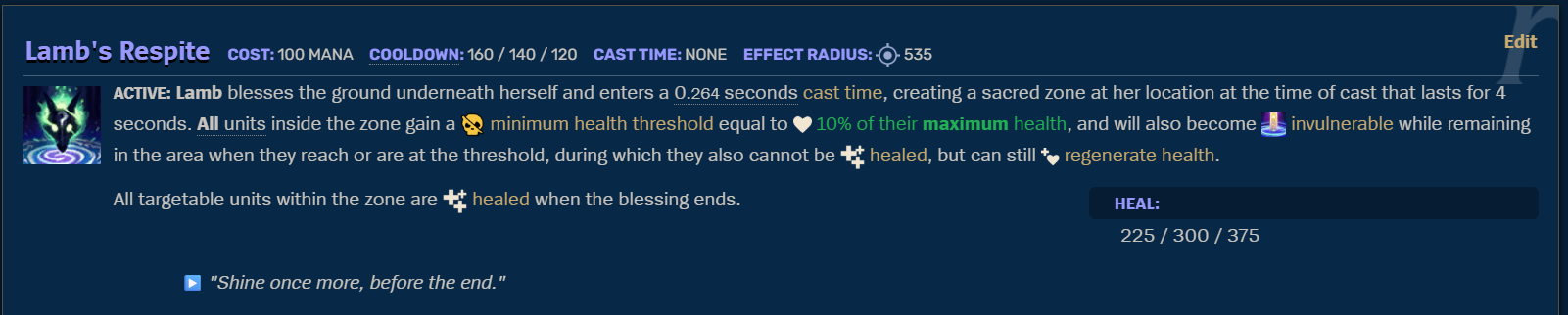
Kindred có một chiêu thức đặc biệt - Cừu cứu sinh (Lamb's Respite).
Cụ thể, trong giao tranh, nếu Hải sử dụng chiêu thức này ngay trước hành động thứ \(l\) và kết thúc ngay sau hành động thứ \(r\), thì HP của tướng không bao giờ dưới \(\lceil\frac{H}{10}\rceil\) trong suốt khoảng thời gian này.
- Nếu HP của tướng ngay trước hành động \(l\) ở dưới hoặc bằng \(\lceil\frac{H}{10}\rceil\) (và còn sống), hoặc HP của tướng sau các hành động từ \(l\) đến \(r\) có thể rơi xuống dưới hoặc bằng \(\lceil\frac{H}{10}\rceil\), thì HP của tướng đó sẽ được đặt thành \(\lceil\frac{H}{10}\rceil\) và giữ nguyên đến khi kết thúc chiêu thức.
- Nếu HP chưa bị khóa ở mức \(\lceil\frac{H}{10}\rceil\) trong lúc chiêu thức đang được sử dụng thì các hành động vẫn có thể tác động tới HP của tướng. Tức chỉ khi HP xuống dưới hoặc bằng mức \(\lceil\frac{H}{10}\rceil\) ở bất kì thời điểm nào trong lúc sử dụng chiêu thức thì mới bị khóa ở mức này.
Ngay sau khi kết thúc chiêu thức, tướng sẽ ngay lập tức được hồi \(y\) máu và tiếp tục các hành động sau đó. \(y\) có thể thay đổi tùy theo chất tướng.
Để giả lập một số tình huống trong game, Hải đưa ra \(q\) truy vấn:
1 l r x y: Tướng ban đầu có HP tối đa là \(x\) và HP ban đầu cũng là \(x\). Hải sử dụng Cừu cứu sinh ngay trước hành động \(l\) và kết thúc ngay sau hành động \(r\). Bạn cần tìm và in ra HP cuối cùng của tướng sau \(n\) hành động, hoặc \(0\) nếu tướng đã chết trong giao tranh.2 x: Tướng ban đầu có HP tối đa là \(x\) và HP ban đầu cũng là \(x\). Trong giao tranh, chiêu thức Cừu cứu sinh có thể chưa được hồi. Vì vậy trong truy vấn này bạn chỉ cần in ra HP của tướng sau \(n\) hành động mà không có Cừu cứu sinh được sử dụng, hoặc \(0\) nếu tướng đã chết trong giao tranh.3 i x: Thay \(a_i\) thành \(x\).
Input (từ file kindred.inp)
- Dòng đầu tiên chứa hai số nguyên dương \(n, q\) \((1 \le n, q \le 3 \times 10^5)\)
- Dòng sau chứa \(n\) số nguyên \(a_1, a_2, \ldots, a_n\) \((-10^9 \le a_i \le 10^9)\).
- \(q\) dòng sau, mỗi dòng chứa một truy vấn thuộc một trong hai dạng:
1 l r x y\((1 \le l \le r \le n, 1 \le x \le 10^9, 0 \le y \le 10^9)\)2 x\((1 \le x \le 10^9\))3 i x\((1 \le i \le n, -10^9 \le x \le 10^9)\)
Output (ra file kindred.out)
Với mỗi truy vấn loại 1 và 3, in ra đáp án tương ứng cho truy vấn đó.
Scoring
- Subtask 1 \((25\%)\): \(n, q \le 5000\);
- Subtask 2 \((20\%)\): Chỉ có truy vấn loại 2;
- Subtask 3 \((20\%)\): Chỉ có truy vấn loại 2 và 3;
- Subtask 4 \((15\%)\): Trong mọi truy vấn loại 1, \(l = r\);
- Subtask 5 \((20\%)\): Không có giới hạn gì thêm.
Chú ý: Nếu sau các truy vấn 2 và 3 mà bạn biết liệu tướng có còn sống hay không nhưng không biết HP cuối cùng sau giao tranh, bạn có thể nhận \(50\%\) số điểm của test đó bằng cách:
- In ra \(-1\) thay cho số HP cuối cùng (hoặc vẫn là \(0\) nếu tướng đã chết).
- Trong một test, nếu bạn chọn trả lời theo hướng này thay vì in ra HP cuối cùng ở một truy vấn bất kì, điểm số cho test đó sẽ là \(50\%\) (nếu đúng) dù cho ở các truy vấn khác bạn vẫn trả lời được HP cuối cùng chính xác.
Example
Test 1
Input
6 5
1 -2 -1 1 0 1
2 4
1 2 4 3 1
3 5 -2
1 2 4 3 1
1 2 4 3 2Output
3
3
0
2Giải thích:
Gọi \(h\) là HP hiện tại của tướng.
Trong truy vấn thứ nhất với \(x = 4\):
| Hành động | HP sau hành động đó |
|---|---|
| 0 | \(h = 4\) |
| 1 | \(4 + 1 = 5\), quá HP tối đa nên vẫn là \(h = 4\) |
| 2 | \(h = 4 - 2 = 2\) |
| 3 | \(h = 2 - 1 = 1\) |
| 4 | \(h = 1 + 1 = 2\) |
| 5 | \(h = 2 + 0 = 2\) |
| 6 | \(h = 2 + 1 = 3\) |
Vậy HP cuối cùng là \(3\).
Sau truy vấn thứ 3, \(a_5 = -2\).
Với truy vấn thứ 4 có \(l = 2, r = 4, x = 3\) và \(y = 1\):
| Hành động | HP sau hành động đó |
|---|---|
| 0 | \(h = 3\) |
| 1 | \(h = 3 + 1 = 4\), quá HP tối đa nên vẫn là \(h = 3\) |
| 2 | \(h = 3 - 2 = 1\), chạm mức \(\lceil\frac{3}{1}\rceil\) nên \(h\) bị khóa đển khi kết thúc chiêu thức (sau \(r = 4\)) |
| 3 | \(h = 1\) |
| 4 | \(h = 1\) |
| Ngay sau kết thúc chiêu thức | \(h = 1 + 1 = 2\) |
| 5 | \(h = 2 - 2 = 0\), tướng đã cạn HP trong giao tranh |
| 6 | \(h = 0\) |
Vậy tướng đã chết trong giao tranh, in ra \(0\).
Về cách tính điểm: Trong test vừa rồi ta có bộ đáp án là \([3, 3, 0, 2]\). Nếu như bạn trả lời \([-1, -1, 0, -1]\) cũng sẽ được chấp nhận và bạn nhận được \(50\%\) số điểm của test này. Nhưng kể cả \([3, 3, 0, -1]\), \([-1, 3, 0, 2]\), ... cũng sẽ chỉ nhận được \(50\%\), còn \([-1, -1, -1, -1]\) là sai và không được điểm.
Fun fact: Lamb's Respite sau khi kết thúc sử dụng sẽ hồi máu cho tất cả các đối tượng trong vùng, kể cả tướng địch, lính, quái rừng, ...