Nguyên rất thích trò chơi xếp tháp. Tòa tháp của Nguyên bao gồm những khối lăng trụ đứng có đáy hình vuông và chiều cao bằng 1. Nguyên sẽ xếp các khối lăng trụ chồng lên nhau để tạo thành một tòa tháp cao.

Mới đây trong lớp học toán, Nguyên được cô giáo dạy về cách tính thể tích các hình khối đơn giản. Nguyên thích thú với kiến thức mới học được và cậu ta muốn tính thể tích tòa tháp của mình.

Tháp của Nguyên bao gồm \(N\) khối lăng trụ đứng chiều cao 1 và có đáy hình vuông và độ dài cạnh đáy từ trên xuống dưới theo thứ tự là \(A_1, A_­­­2, ... A_­­N.\) Dãy \(A\) được tạo như sau:

• \(A_1 = 1.\)
• \(A_2\) sẽ là một số dương tùy ý mà Nguyên chọn trong mỗi lần chơi để tránh nhàm chán.
• \(A_i (i > 2)\) bằng \(2 × A_2 × A_{i-1}–A_{i-2}\)

Nguyên biết rõ thể tích hình một hình lăng trụ sẽ bằng chiều cao nhân với diện tích đáy nhưng vì ngại tính toán, Nguyên muốn nhờ bạn viết một chương trình giúp cậu ta. Kết quả có thể rất lớn vì vậy bạn chỉ cần ghi ra theo \(\mod M\) với \(M\) là một số nguyên dương cho trước.

Input

• Dòng 1: Ghi số nguyên dương \(K \le 10\) là số bộ dữ liệu.
• \(K\) dòng tiếp: Mỗi dòng ghi 3 số nguyên \(A_2, N, M\) tương ứng với một bộ dữ liệu. (\(1 \le A_2, M \le 10^9, 2\le N \le 10^9\))

Output

• Với mỗi bộ test ghi ra một số duy nhất là kết quả tương ứng trên một dòng.

Example

2
1 10 1000
2 3 100 

10
54

Để chuẩn bị tốt cho vai diễn người nhện của mình, Tôm Hà Lan quyết định luyện tập đi dây. Khu phố anh đang ở có \(n\) tòa nhà, tòa nhà thứ \(i\) cao \(a_i\) mét . Xuất phát từ tòa nhà đầu tiên, Tôm Hà Lan muốn đu đến tòa nhà thứ \(n\) . Biết rằng anh ta chỉ có thể đu từ tòa nhà \(i\) tới toà nhà \(j\) nếu \(i<j\) và \(\gcd(a_i,a_j)>1\), hãy đếm số cách đu dây có thể của anh chàng này.

Input

• Dòng đầu tiên là số nguyên dương \(n\) \((n \le 2 \times 10^5)\).
• Dòng thứ hai là \(n\) số nguyên dương \(a_i\) \((a_i \le 5 \times 10^5)\).

Output

• Gồm một dòng duy nhất là số cách đu dây chia dư cho \(10^9 + 7\).

Scoring

• Subtask \(1\): \(n \le 1000\).
• Subtask \(2\): Không có thêm điều kiện

Example

5
2 6 3 4 6

5

5
4 196 2662 2197 121

2

7
3 6 8 9 11 12 20

7

Limak, như bao người khác, lúc vui lúc buồn. Cảm xúc của anh thay đổi khi anh đọc một chuỗi gồm các chữ cái in hoa tiếng Anh.

• Chữ S hoặc D luôn làm Limak buồn, bất kể trước đó anh đang vui hay buồn.
• Chữ H làm Limak vui.
• Các nguyên âm A, E, I, O, U làm đảo ngược cảm xúc hiện tại (vui \(\leftrightarrow\) buồn).
• Những chữ cái còn lại không làm thay đổi cảm xúc.
  Ban đầu Limak đang vui. Với mọi xâu độ dài \(n\) trên bảng chữ cái 26 ký tự in hoa, hãy đếm số xâu mà sau khi đọc xong Limak vẫn vui. In kết quả theo modulo \(10^9+7\).

Input

• Một số nguyên dương \(n\) (\(1 \le n \le 10^{18}\)).

Output

• In ra đáp án modulo \(10^9+7\).

1

19

2

403

11

145418665

Cho một mảng hai chiều vô hạn \(F\) được định nghĩa như sau:

• \(F_{0,0} = 0\),
• \(F_{0,1} = F_{1,0} = 1\),
• Với mọi \(i \ge 2\), \(F_{i,0} = F_{i-1,0} + F_{i-2,0}\),
• Với mọi \(j \ge 2\), \(F_{0,j} = F_{0,j-1} + F_{0,j-2}\),
• Với mọi \(i,j \ge 1\), \(F_{i,j} = F_{i-1,j} + F_{i,j-1}\).

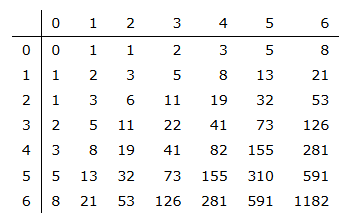
Dưới đây là một vài giá trị đầu của \(F\) (các chỉ số hàng và cột từ 0):

Cho hai số nguyên không âm \(x,y\) với \(0 \le x,y < 10^6\). Hãy tính giá trị \(F_{x,y}\) và in kết quả modulo \(10^9+7\).

Input

• Một dòng duy nhất gồm hai số nguyên \(x\) và \(y\) (\(0 \le x,y < 10^6\)).

Output

• In ra một số nguyên --- giá trị \(F_{x,y} \bmod (10^9+7)\).

2 2

6

1 5

13

Cho hai dãy số nguyên \(a_1,\dots,a_N\) và \(b_1,\dots,b_M\).
Gọi \(c_1,\dots,c_k\) là một dãy con chung (không cần liên tiếp) của cả hai dãy trên.
Đặt

Hãy xác định dãy con chung có giá trị \(f\) lớn nhất và in ra giá trị đó.

Input

• Dòng đầu: hai số nguyên \(N\) và \(M\).
• Dòng thứ hai: \(N\) số nguyên biểu diễn dãy \(A\).
• Dòng thứ ba: \(M\) số nguyên biểu diễn dãy \(B\).

Output

• Một số nguyên duy nhất là giá trị lớn nhất của \(f\).

Scoring

• Trong tất cả các test: \(1\le N,M\le 5000\), và \(-10^9 \le a_i,b_i \le 10^9\).

    4 4
    1 15 8 7
    15 1 7 8

    8