Cho một số nguyên dương \(a\).
Hãy in tam giác sao gồm các ký tự * sao cho:

• Hàng đầu tiên có \(a\) dấu *;
• Hàng thứ hai có \(a - 1\) dấu *;
• ...
• Hàng cuối cùng có 1 dấu *.

Mỗi hàng được in trên một dòng riêng, không có ký tự thừa ở đầu hoặc cuối dòng.

Input

• Một dòng duy nhất chứa số nguyên \(a\) \((1 \le a \le 1000)\).

Output

• In \(a\) dòng, trong đó dòng thứ \(i\) \((1 \le i \le a)\) chứa đúng \(a - i + 1\) ký tự *.
  Mỗi dòng kết thúc bằng ký tự xuống dòng.

Examples

5

*****
****
***
**
*

1

*

Cho một số nguyên dương \( n \).
Xét giai thừa của \( n \), ký hiệu là \( n! = 1 \times 2 \times 3 \times \dots \times n \).

Yêu cầu: Đếm số lượng chữ số \( 0 \) liên tiếp ở cuối biểu diễn thập phân của \( n! \).

Input

• Một dòng duy nhất chứa số nguyên \( n \) \((1 \le n \le 10^6)\).

Output

• In ra một số nguyên duy nhất — là số lượng chữ số \( 0 \) tận cùng của \( n! \).

Examples

10

2

5

1

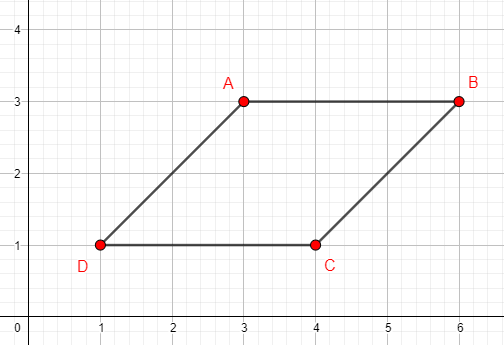
Cho bốn đỉnh của một tứ giác lồi trên mặt phẳng tọa độ \(Oxy\), lần lượt theo chiều kim đồng hồ:
\(A(x_1, y_1)\), \(B(x_2, y_2)\), \(C(x_3, y_3)\), \(D(x_4, y_4)\).
Hãy tính diện tích của tứ giác đó.

Input

• Gồm 4 dòng, dòng thứ \(i\) chứa hai số nguyên \(x_i, y_i\) (\(|x_i|, |y_i| \le 100\)).

Output

• In ra diện tích của tứ giác, sai số cho phép không vượt quá \(10^{-3}\).

Examples

3 3 
6 3
4 1
1 1

6

0 0
1 5
5 4
5 0

20.499999999999996

Scoring

• Subtask 1 (50% số điểm): Tứ giác là hình chữ nhật hoặc hình bình hành.
• Subtask 2 (50% số điểm): Tứ giác bất kỳ (vẫn lồi).

Cho một số nguyên dương \(n\). Hãy đếm số bộ gồm bốn số nguyên dương \((x_1, x_2, x_3, x_4)\) thỏa mãn:

• \(x_1 < x_2 < x_3 < x_4\).
• \(x_1 + x_2 + x_3 + x_4 = n\).

Input

• Một dòng duy nhất chứa số nguyên dương \(n\) (\(1 \le n \le 50\)).

Output

• In ra một số nguyên là số lượng bộ \((x_1, x_2, x_3, x_4)\) thỏa mãn điều kiện đã cho.

Examples

10

1

15

6

Cho một ma trận có kích thước \(n \times m\), hãy in ra toàn bộ phần tử của ma trận theo đường chéo zigzag.
Cụ thể: bắt đầu từ phần tử ở góc trên bên trái \((1,1)\), di chuyển theo các đường chéo luân phiên hướng lên-phải và xuống-trái, cho đến khi in hết các phần tử và kết thúc tại \((n,m)\).

Input

• Dòng đầu tiên chứa hai số nguyên \(n, m\) (\(1 \le n, m \le 1000\)).
• \(n\) dòng tiếp theo, mỗi dòng chứa \(m\) số nguyên \(A_{i,j}\) (\(1 \le A_{i,j} \le 100\)), biểu diễn các phần tử của ma trận.

Output

• In ra dãy gồm \(n \times m\) số nguyên theo thứ tự đường chéo zigzag, cách nhau bởi một dấu cách.

Subtasks

• Subtask 1 (30% số điểm): \(1 \le n, m \le 50\)
• Subtask 2 (70% số điểm): \(1 \le n, m \le 1000\)

Examples

3 3
1 2 3
4 5 6
7 8 9

1 2 4 7 5 3 6 8 9

2 4
1 2 3 4
5 6 7 8

1 2 5 6 3 4 7 8

Đằng sau một lập trình viên thành công là một cô bạn gái... không tồn tại 🗿

Nhân dịp sinh nhật, Tèo được thưởng một chiếc điện thoại Nakio. Một ngày nọ, mải chụp ảnh up story, cậu vô tình làm rơi chiếc điện thoại của mình làm cho bàn phím của nó hoạt động một cách rất ảo diệu. Khi nhấn vào một phím, chiếc điện thoại lại hiện ra các ký tự của phím khác. May mắn thay là không có hai phím nào hoạt động giống nhau nên Tèo vẫn có thể viết được tất cả các chữ cái. Sau một hồi tìm hiểu, cậu ấy đã tìm được cách hoạt động của các phím.

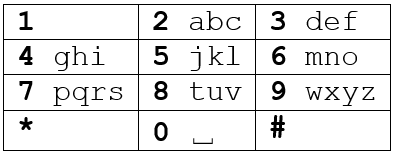
Đây là cách thức hoạt động của bàn phím điện thoại khi nó vẫn chưa bị hỏng. Bàn phím hoạt động gần tương tự với bộ gõ T9 trên những chiếc điện thoại cục gạch quen thuộc của nhiều thế hệ.
Muốn gõ được chữ a, ta cần nhấn phím 2 một lần; muốn gõ được chữ b, ta cần nhấn phím 2 hai lần.
Nếu muốn viết hai chữ cái nằm trên cùng một phím thì sau khi gõ chữ cái đầu tiên, ta cần nhấn phím # một lần rồi sau đó gõ chữ cái tiếp theo.
Ví dụ, muốn viết xâu abc, ta cần nhấn theo thứ tự 2#22#222.
Phím 0 hoạt động như dấu cách, 1 và * không hoạt động.

Tèo vừa chia tay với người yêu nên cậu ấy muốn up story suy suy thất tình lên mạng xã hội F bằng chiếc điện thoại của mình.
Hãy chỉ ra thứ tự các phím cần nhấn để viết được dòng caption đó.

Input

• Dòng đầu tiên chứa 9 số nguyên phân biệt từ 1 đến 9 có ý nghĩa:
  Số thứ 1 là cách hoạt động của phím 1, số thứ 2 là cách hoạt động của phím 2, ..., số thứ 9 là cách hoạt động của phím 9.
  (Nghĩa là nếu số thứ 2 là 3 thì lúc này phím 2 sẽ hoạt động như phím 3).
• Dòng thứ hai là một xâu gồm các chữ cái tiếng Anh viết thường (có thể có dấu cách) có độ dài không quá 100, là nội dung của story mà Tèo muốn up lên trang F.
  Dữ liệu đảm bảo sau ký tự cuối cùng của caption không có dấu cách.

Output

Một xâu mô phỏng thứ tự các phím cần nhấn để viết được dòng caption của Tèo.

Scoring

• Subtask 1 [50%]: Bàn phím của Tèo không bị hỏng.
  (Nói cách khác, ở dòng đầu tiên, số thứ i có giá trị là i với 1 ≤ i ≤ 9.)
• Subtask 2 [50%]: Không có ràng buộc gì thêm.

Examples

1 2 3 4 5 6 7 8 9
den do roi kia minh dung lai em nhe

3#3366036660777666444055444206444664403886640555244403360664433

4 6 2 5 1 7 9 3 8
nhin sang trai vi em khong phai cua anh

2211#111220666632210966631110999111088204411222#221061131110333993032211

Cho hai số nguyên dương \(a\) và \(b\).
Hãy tính tổng tất cả các số nguyên dương \(x\) thỏa mãn đồng thời:

• \(x\) là ước của \(a\).
• \(3x\) là ước của \(b\).

Nếu không tồn tại giá trị \(x\) nào thỏa mãn, kết quả được xem là \(0\).

Input

• Một dòng duy nhất chứa hai số nguyên dương \(a, b\) (\(1 \le a, b \le 10^{12}\)).

Output

• In ra tổng tất cả các số nguyên dương \(x\) thỏa mãn điều kiện trên.
  Dữ liệu đảm bảo kết quả không vượt quá \(10^{18}\).

Examples

4 18

3

1 2

0

Scoring

• Subtask 1 (80% số điểm): \(1 \le a,b \le 10^6\).
• Subtask 2 (20% số điểm): Không có ràng buộc gì thêm .

Có \(n\) drone được đánh số liên tiếp từ \(L\) đến \(L + n - 1\).
Danh sách hiện tại chỉ còn \(n - 1\) số hiệu do một drone bị mất.
Hãy xác định số hiệu của drone bị thiếu.

Input

• Dòng đầu tiên chứa hai số nguyên \(n, L\) (\(1 \le n \le 10^5\), \(1 \le L \le 10^9\)).
• Dòng thứ hai chứa \(n - 1\) số nguyên, là danh sách số hiệu của các drone còn lại.

Output

• In ra một số nguyên duy nhất, là số hiệu của drone bị thiếu.

Examples

5 1
5 1 3 2

4

5 100
104 102 103 100

101

Scoring

• Subtask 1 (70% số điểm): \(n \le 10\), \(L \le 10\).
• Subtask 2 (30% số điểm): Không có ràng buộc gì thêm. (trùng global constraint)

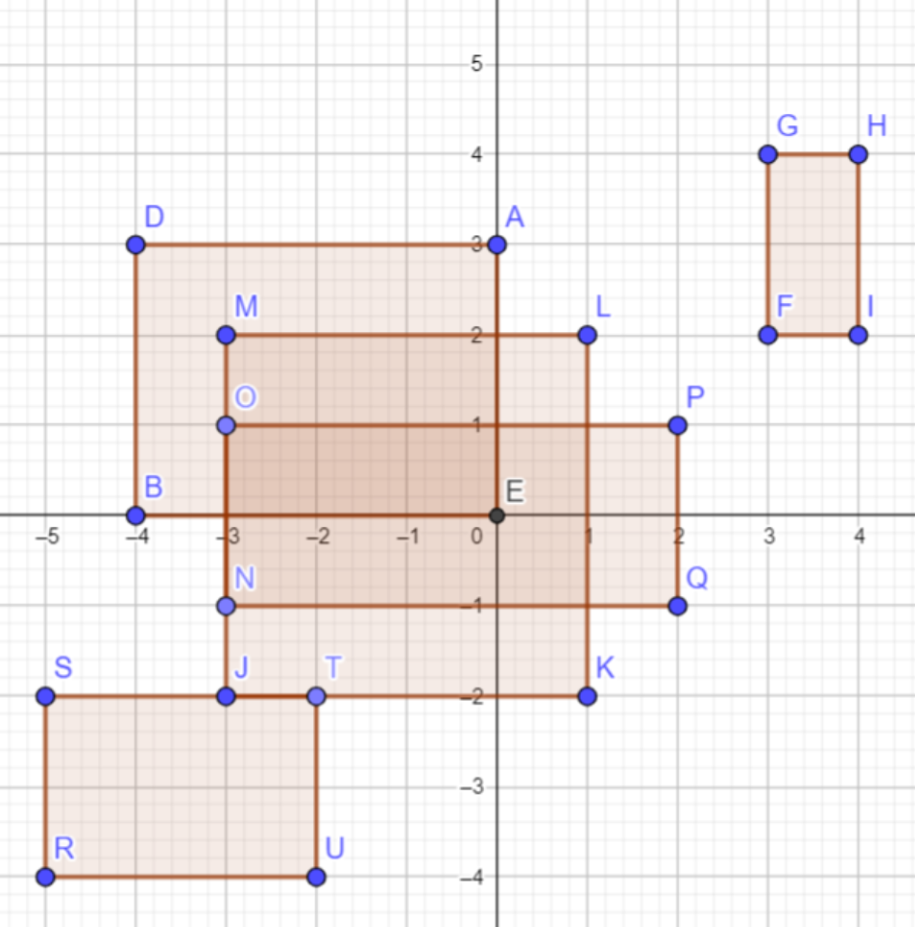
Cho N hình chữ nhật được xác định bằng hai điểm góc trái dưới và phải trên. Hãy đếm xem có bao nhiêu cặp hình chữ nhật có điểm chung (không bao gồm chạm cạnh hoặc chạm đỉnh).

INPUT

• Dòng đầu tiên chứa một số nguyên dương N (N ≤ 1000)
• N dòng tiếp theo, mỗi dòng gồm 4 số nguyên: x1, y1, x2, y2 mô tả tọa độ góc trái dưới và góc phải trên của một hình chữ nhật.

Các giá trị tọa độ có trị tuyệt đối không vượt quá 10⁹.

OUTPUT

In ra một số nguyên duy nhất — là số cặp hình chữ nhật có điểm chung.

Ví dụ

Giải thích minh họa

Hình minh họa cho thấy trong 5 hình chữ nhật được cho, chỉ có 3 cặp hình chữ nhật có phần giao nhau (có điểm chung).

Một công ty cần mua \(N\) lít sữa. Có \(M\) người nông dân cung cấp sữa, người nông dân thứ \(i\) có \(A_i\) lít sữa và bán với giá \(P_i\) cho mỗi lít.

Công ty có thể mua sữa từ nhiều người nông dân khác nhau. Hãy tính số tiền ít nhất mà công ty cần bỏ ra để mua đủ \(N\) lít sữa. Dữ liệu đảm bảo tổng lượng sữa của tất cả nông dân luôn lớn hơn hoặc bằng \(N\).

Input

• Dòng đầu tiên chứa hai số nguyên \(N\) và \(M\) (\(0 \le N \le 10^9\), \(1 \le M \le 10^6\)), lần lượt là tổng số lít sữa cần mua và số lượng người nông dân.
• \(M\) dòng tiếp theo, mỗi dòng chứa hai số nguyên \(P_i\) và \(A_i\) (\(0 \le P_i \le 10^9\), \(1 \le A_i \le 10^9\)), lần lượt là giá 1 lít sữa và lượng sữa mà người nông dân thứ \(i\) có.

Output

• In ra một số nguyên duy nhất là tổng chi phí nhỏ nhất để mua đủ \(N\) lít sữa.

Examples

100 5
5 20
9 40
3 10
8 20
6 30

650

10 3
3 5
2 8
4 10

22

Scoring

• Subtask 1 (40% số điểm): \(N \le 10^6, A_i \le 10^6\).
• Subtask 2 (60% số điểm): Không có ràng buộc gì thêm.

Cho ba số nguyên dương \(a, l, r\) thỏa mãn \(1 \le a \le 10^{10}\) và \(1 \le l \le r \le 10^{10}\).

Yêu cầu:
Tìm giá trị lớn nhất của \(a \bmod i\) khi \(i\) chạy từ \(l\) đến \(r\).
Ký hiệu \(a \bmod i\) là phần dư của phép chia \(a\) cho \(i\).

Input

• Dòng đầu tiên chứa số nguyên \(T\) (\(1 \le T \le 10\)), là số bộ test.
• Mỗi trong \(T\) dòng tiếp theo chứa ba số nguyên \(a, l, r\).

Output

• Với mỗi test, in ra một số nguyên duy nhất là giá trị lớn nhất của \(a \bmod i\) trong đoạn \([l, r]\).

Examples

1
15 4 10

7

2
21 11 89
5 5 5

21
0

Scoring

• Subtask 1 (30% số điểm): \(1 \le a, l, r \le 10^5\).
• Subtask 2 (70% số điểm): \(1 \le a, l, r \le 10^{10}\).

Phát minh mới nhất của của Nitori là một chiếc máy bay ném bom điều khiển từ xa. Ba nàng tiên ánh sáng đã đặt một chiếc cho kế hoạch khủng bố đền Hakurei.

Dĩ nhiên để máy bay có thể hoạt động thì cần có pin. Mỗi cục pin có 3 thông tin: \(e_i, w_i, c_i\) lần lượt và mức năng lượng, khối lượng và giá thành. Thời gian bay của máy bay được xác định bằng công thức: \(E\over{W}\) trong đó \(E\) là tổng mức năng lượng và \(W\) là tổng khối lượng của tất cả pin và khối lượng của máy bay.

Để đảm bảo kế hoạch thành công, máy bay cần hoạt động lâu nhất có thể. Ba nàng tiên có ngân sách \(b\) và khối lượng của máy bay là \(w\), hãy giúp họ chọn pin sao cho thời gian bay là lâu nhất!

Input:

• Dòng đầu chứa số \(n,b,w (1≤n×b≤10^5,1≤w≤1000)\).
• \(n\) dòng tiếp theo mỗi dòng chứa ba số \(e_i,w_i,c_i (0≤e_i,w_i≤1000,0≤c_i≤b)\) là mức năng lượng, khối lượng và giá thành của cục pin thứ \(i\).

Output:

• In ra tổng thời gian bay của máy bay, sai số không quá \(10^{-3}\).

Sample Test:

10 1000 20
40 40 40
1 1 1
70 30 60
100 20 700
80 50 200
30 1 200
100 100 1
20 1 500
30 20 100
70 50 100

3.1707

Giới hạn

• 25% số điểm \(n≤20\).
• 25% số điểm \(w_i=0\).
• 25% số điểm \(c_1=c_2=...=c_n\).
• 25% số điểm không có ràng buộc gì thêm.