HSG THPT Vòng 1 Hà Nội 2020
Đếm Đoạn
Nộp bàiNguồn: Học sinh Giỏi THPT Hà Nội năm 2019 - 2020
Cho số nguyên dương \(N\). Đếm xem có bao nhiêu cặp số nguyên \([a,b]\) \((0 < a \le b)\) để tổng các số nguyên trong đoạn \([a,b]\) bằng \(N\). Hai đoạn khác nhau là hai đoạn có ít nhất một phần tử khác nhau.
Input
Dữ liệu vào từ tệp văn bản BAI1.INP:
- Gồm một dòng duy nhất chứa số nguyên dương \(N\).
Output
Kết quả ra tệp văn bản BAI1.OUT:
- Gồm một dòng duy nhất là kết quả bài toán.
Example
Test 1
Input
9Output
3Note
- Có ba đoạn số thoả mãn: \([2, 4],[4, 5],[9, 9].\)
Constraint
- Có \(40\%\) số điểm tương ứng với \(N \leq 10^4\).
- Có \(30\%\) số điểm tương ứng với \(10^4 < N \leq 10^8\).
Số đặc biệt
Nộp bàiNguồn: Học sinh Giỏi THPT Hà Nội năm 2019 - 2020
Số đặc biệt là một số nguyên dương \(N\) sao cho khi thêm chữ số \(a\) vào đầu và chữ số \(b\) vào cuối số \(N\) sẽ được số mới có giá trị gấp \(k\) lần số \(N\) ban đầu, tức là \(aNb = k \times N\).
Yêu cầu: Cho trước ba số nguyên \(a, b, k\). Tìm số đặc biệt \(N\) (\(N \leq 10^{18}\)).
Input
Dữ liệu vào từ tệp văn bản BAI2.INP:
- Gồm một dòng ghi ba số \(a, b, k\) (\(0 \leq a, b \leq 9\); \(10 \leq k \leq 200\)) cách nhau một dấu cách.
Output
Kết quả ra tệp văn bản BAI2.OUT:
- Gồm một số \(N\) duy nhất là kết quả của bài toán. Trong trường hợp có nhiều hơn một số \(N\) thỏa mãn, hãy đưa ra số bé nhất. Cho biết với dữ liệu vào, luôn tồn tại kết quả.
Example
Test 1
Input
4 5 91Output
5Note
- 91 \(\times\) 5 = 455
Constraint
- Có \(50\%\) số điểm tương ứng với \(N \leq 10^9\)
Sắp xếp
Nộp bàiNguồn: Học sinh Giỏi THPT Hà Nội năm 2019 - 2020
Cho một dãy số có \(N\) phần tử \(a_1, a_2, ..., a_N\). Dãy số đẹp bậc \(K\) là được mô tả như sau:
-
Dãy số có \(K\) nhóm, mỗi nhóm có số phần tử bằng nhau. \(N/K\) phần tử đầu tiên của dãy số (từ \(a_1\) đến \(a_{N/K}\)) vào nhóm \(1\), \(N/K\) phần tử tiếp theo vào nhóm \(2\), ..., \(N/K\) phần tử cuối cùng vào nhóm \(K\).
-
Nhóm \(1\) \(\geq\) nhóm \(2\) \(\geq\) \(\cdots\) \(\geq\) nhóm \(K\) với nhóm \(i\) \(\geq\) nhóm \(j\) khi phần tử nhỏ nhất của nhóm \(i\) lớn hơn hoặc bằng phần tử lớn nhất của nhóm \(j\).
Yêu cầu: Ta cần di chuyển số lần nhỏ nhất các phần tử của dãy số ban đầu để trở thành dãy số đẹp bậc \(K\). Cách di chuyển một phần tử là lấy phần tử đó ra khỏi dãy số sau đó chèn vào một vị trí bất kỳ trong dãy số.
Input
Dữ liệu vào từ tệp văn bản BAI3.INP:
- Dòng đầu tiên chứa hai số nguyên dương \(N\) và \(K\) (\(0 < K \leq N \leq 10^5\), \(N\) chia hết cho \(K\)).
- Dòng thứ hai chứa \(N\) số nguyên dương \(a_i\) (\(|a_i| \leq 10^9\)).
Output
Kết quả ra tệp văn bản BAI3.OUT:
- Ghi ra tổng số lần di chuyển ít nhất thoả mãn yêu cầu bài toán.
Example
Test 1
Input
4 2
5 1 9 4Output
1Note
- Di chuyển số 1 xuống cuối dãy:
5 9 4 1
Constraint
- Có \(50\%\) số điểm tương ứng với \(10 < N \leq 5000.\)
Tìm đường
Nộp bàiNguồn: Học sinh Giỏi THPT Hà Nội năm 2019 - 2020
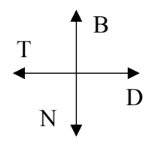
Trung tâm khảo sát hang động XYZ có một robot tự hành. Robot này có thể tự di chuyển, vẽ sơ đồ, chụp các hình ảnh trong lòng hang động và truyền các thông tin về trung tâm. Thông tin về đường đi trong hang động được gửi về trung tâm chuỗi các chữ cái \(D, T, N, B\) tương ứng với việc đi theo các hướng Đông, Tây, Nam, Bắc trên la bàn được gắn trên robot (trong một đơn vị khoảng cách, hướng đi không thay đổi quy chiếu trên mặt phẳng nằm ngang với mặt đất, các hướng đi quy định ở hình bên).
Trong một lần robot thực hiện nhiệm vụ khảo sát một hang động mới, sau một thời gian di chuyển (trong quá trình di chuyển một điểm trong hang có thể được robot đi qua, đi lại nhiều lần) và truyền thông tin về trung tâm, robot gặp sự cố và không thể di chuyển về điểm xuất phát là cửa hang. Trung tâm muốn đưa robot về cửa hang bằng cách sử dụng những đoạn đường an toàn mà robot đã đi qua một cách nhanh nhất.
Yêu cầu: Cho chuỗi ký tự là thông tin đường đi của robot đã gửi về trung tâm. Hãy tìm độ dài đường đi ngắn nhất từ cửa hang đến được vị trí của robot bằng sử dụng thông tin đường đi trên.
Input
Dữ liệu vào từ tệp văn bản BAI4.INP:
- Một dòng gồm chuỗi các ký tự \(D, T, N, B\) ghi liên tiếp nhau. Số ký tự không quá \(10000\).
Output
Kết quả ra tệp văn bản BAI4.OUT:
- Độ dài đường đi ngắn nhất tìm được.
Example
Test 1
Input
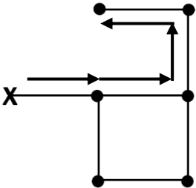
DDTNDBBTOutput
4Note
Constraint
- Có \(50\%\) số test độ dài xâu nhỏ hơn hoặc bằng \(1000.\)