Nguồn: Học sinh Giỏi THPT Hà Nội năm 2023 - 2024

Một công ty gồm \(N\) người được đánh số từ \(1\) tới \(N\). Tổng giám đốc của công ty được đánh số là \(1\), mỗi người từ \(2\) tới \(N\) có đúng một cấp trên trực tiếp của mình.

Nếu \(i\) là cấp trên trực tiếp của \(j\), ta gọi \(i\) là quản lý của \(j\). Nếu \(i\) là quản lý của \(j\) thì \(i\) cũng là quản lý của những người mà \(j\) quản lý. Không có trường hợp \(i\) là quản lý của \(j\) đồng thời \(j\) là quản lý của \(i\).

Công ty có chế độ lương thưởng rất đặc biệt, người thứ \(i\) có lương là \(a_i\), người cấp dưới có thể có lương cao hơn người quản lý.

Công ty muốn tổ chức một sự kiện cho toàn bộ công ty. Nhưng nếu hai người \(u\) và \(v\) tham gia, trong đó \(u\) là quản lý của \(v\) mà lương của \(u\) không cao hơn lương của \(v\) \((a_u \le a_v)\) thì sẽ gây ra bất hoà. Công ty muốn chọn ra được nhiều người nhất tham gia sự kiện mà không có sự bất hoà nào.

Phòng tổ chức sự kiện đã lên \(Q\) giả định như sau: Xét người \(u \ (1 \le u \le N)\), chọn ra một số người mà \(u\) là quản lý (có thể chọn hoặc không chọn \(u\)) để tham gia sự kiện sao cho:

• Tổng số người được chọn là lớn nhất;
• Không có sự bất hoà nào giữa những người được chọn.

Yêu cầu: Với mỗi giả định, in ra số người nhiều nhất có thể chọn để tham gia sự kiện.

Input

Dữ liệu vào từ tệp văn bản CONGTY.INP:

• Dòng đầu tiên chứa hai số nguyên dương \(N\) và \(Q\) \((1 \le N, Q \le 2 \times 10^5)\);
• Dòng thứ hai gồm \(N\) số nguyên dương, số thứ \(i\) là \(a_i\) mô tả mức lương của người thứ \(i\) \((1 \le a_i \le 10^9)\);
• Dòng thứ ba gồm \(N - 1\) số nguyên dương, số thứ \(i\) là \(p_i\) mô tả \(p_i\) là cấp trên trực tiếp của \(i+1\) \((1 \le p_i \le N)\);
• \(Q\) dòng sau, dòng thứ \(i\) gồm một số nguyên dương \(u_i \ (1 \le u_i \le N)\), mô tả giả định thứ \(i\).

Output

Kết quả ra tệp văn bản CONGTY.OUT:

• Với mỗi giả định, in ra kết quả tương ứng.

Examples

6 3
8 4 2 7 1 3
1 1 3 2 3
1
3
4

5
2
1

6 2
7 5 6 4 3 1
1 1 3 3 5
3
1

4
6

Note

• Ví dụ 1: Hình vẽ minh hoạ như Hình 3.
  

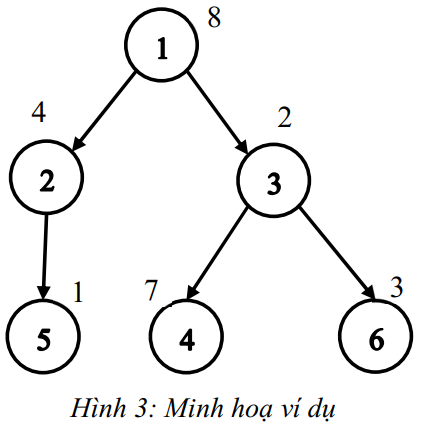
  • Với giả định thứ nhất, chọn các nhân viên: \(1, 2, 5, 4, 6\);
  • Với giả định thứ hai, chọn các nhân viên: \(4, 6\);
  • Với giả định thứ ba, chọn nhân viên: \(4\).

• Ví dụ 2:

  • Với giả định thứ nhất, chọn các nhân viên: \(3, 4, 5, 6\);
  • Với giả định thứ hai, chọn các nhân viên: \(1, 2, 3, 4, 5, 6\).

Constraint

• Có \(40\%\) số test ứng với \(40\%\) số điểm của bài thoả mãn: \(M = 1; \ N, D \le 10^3\);
• \(20\%\) số test khác ứng với \(20\%\) số điểm của bài thoả mãn: \(M = 1; \ N \le 10^5\);
• \(20\%\) số test khác ứng với \(20\%\) số điểm của bài thoả mãn: \(2 \le M, N \le 1000;\) số khu dân cư, số siêu thị không vượt quá \(1000\);
• \(20\%\) số test còn lại ứng với \(20\%\) số điểm của bài thoả mãn: \(2 \le M, N \le 1000\).